
Wiederholung
Bei einem Fest wird ein Feuerwerk arrangiert. Die einzelnen Raketen sind durch gleich lange Zündschnüre miteinander verbunden (siehe Bild). Die blaue Rakete wird entzündet.
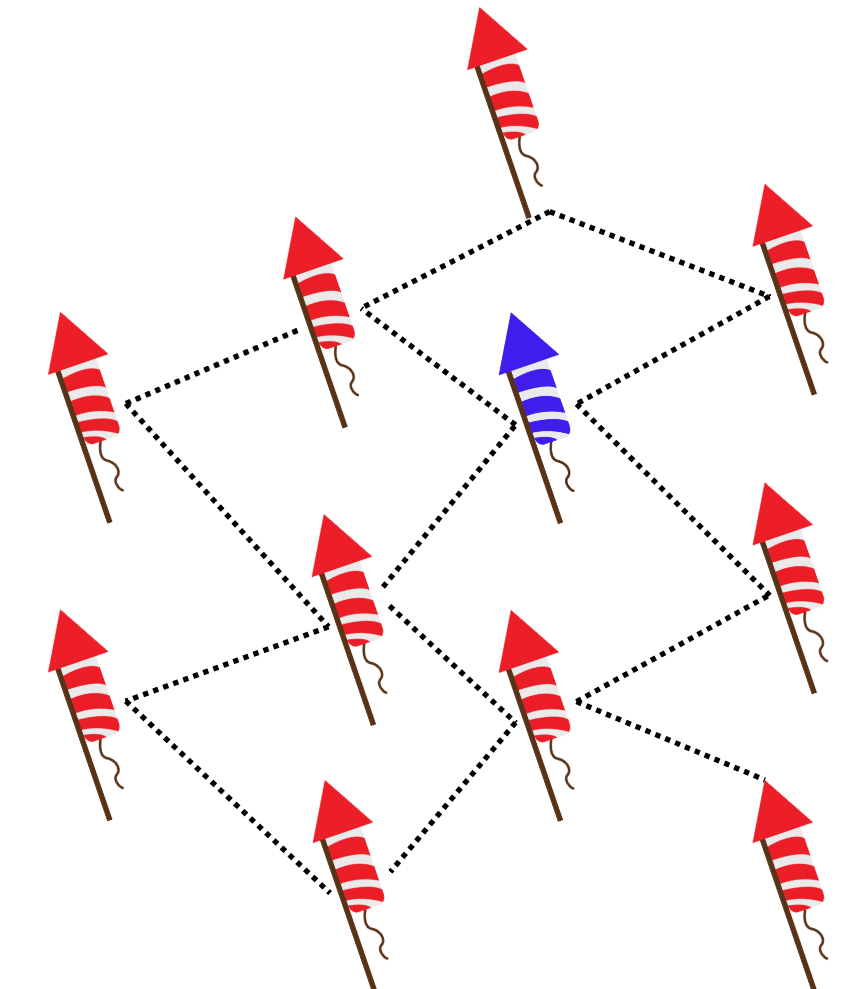
- Erstelle einen Graphen für dieses Szenario.
- Markiere mit einem Pfeil, welche Rakete eine andere startet. Sollten zwei Raketen eine starten, reicht ein Pfeil aus.
- Jede Zündschnur brennt eine Sekunde lang. Notiere neben den Raketen die Zeit, zu der sie entzündet wird.
Entdecken
Du hast gerade die Breitensuche durchgeführt! Überprüfe deine Ergebnisse mit der folgenden Seite.<– Klick
Gibt es eine bessere Startrakete? Begründe! (Ja, schriftlich)
Zusammenhang
Zeichne hier (<– Klick) zwei unabhängige Feuerwerke ein und starte die Breitensuche. Was fällt dir auf?
Hefteintrag
(Ja, abschreiben…)
1.4 Die Breitensuche
Übung
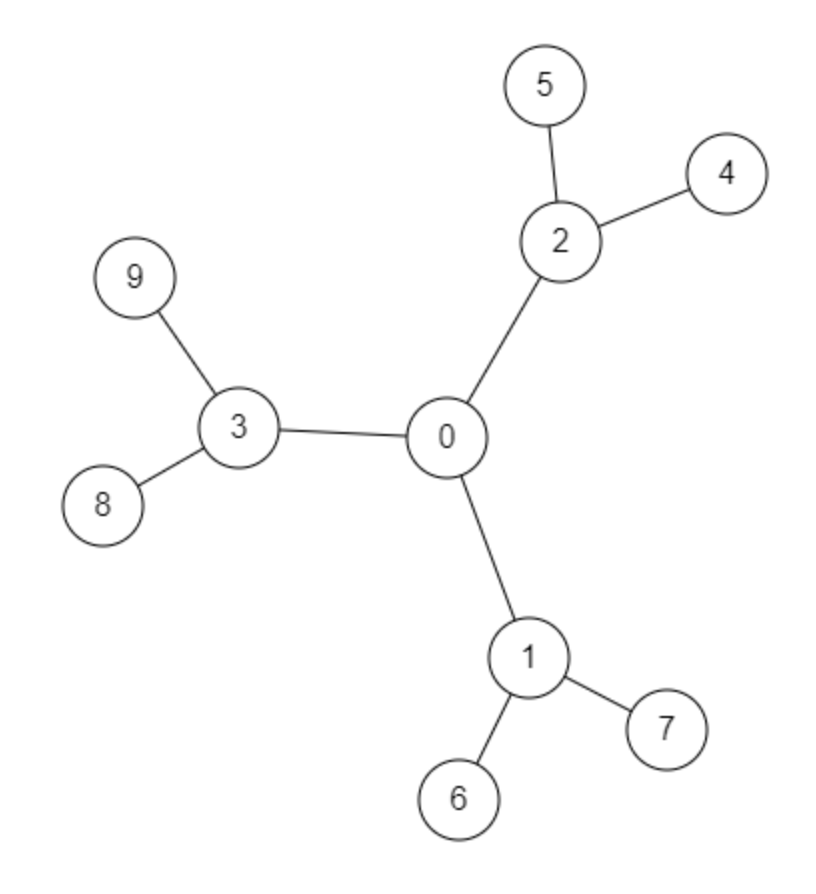
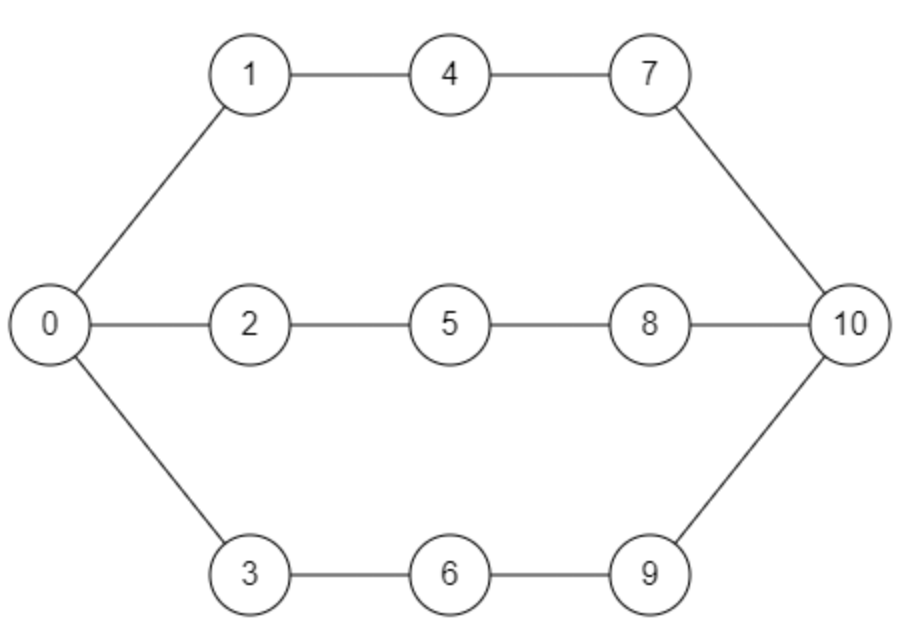
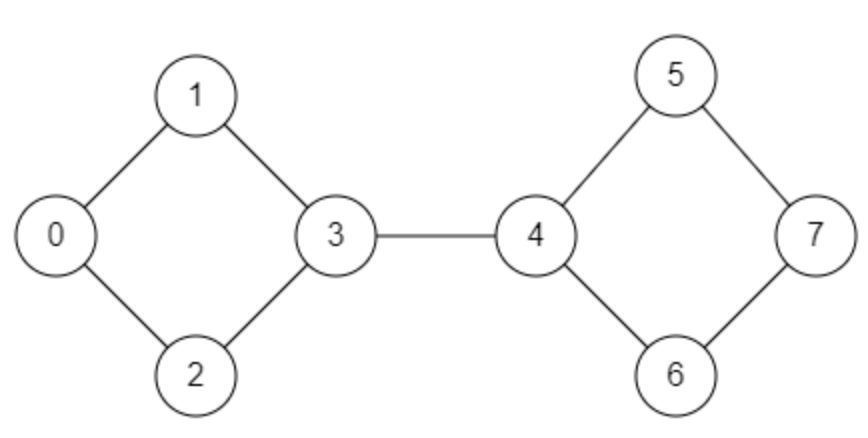
Führe für folgende Graphen die Breitensuche mit Start 0
- erst analog (Pfeile und Entfernungen notieren) und
- DANACH digital durch, um deine Lösungen zu überprüfen
Algorithmus verstehen
In der Animation sieht es so aus, als ob der Algorithmus mehrere Knoten auf einmal entdeckt. Ein Algorithmus kann jedoch nur eine Sache gleichzeitig erledigen. Deshalb muss er Informationen speichern:
- Aktueller Knoten: Dies ist der Knoten, den der Algorithmus gerade betrachtet.
- Warteschlange: Hier werden die Knoten gespeichert, die noch bearbeitet werden müssen. Der Algorithmus nimmt sich immer den ersten Knoten aus der Warteschlange vor.
- entdeckte Knoten: Dies sind die Knoten, die der Algorithmus bereits entdeckt hat.
Hier (<– Klick) kannst du die gerade analysierten Graphen Schritt für Schritt durchgehen. Klicke unten auf „Standardgraph“ um die Graphen zu laden.
Erklären
Das ist der Graph „Gitter“
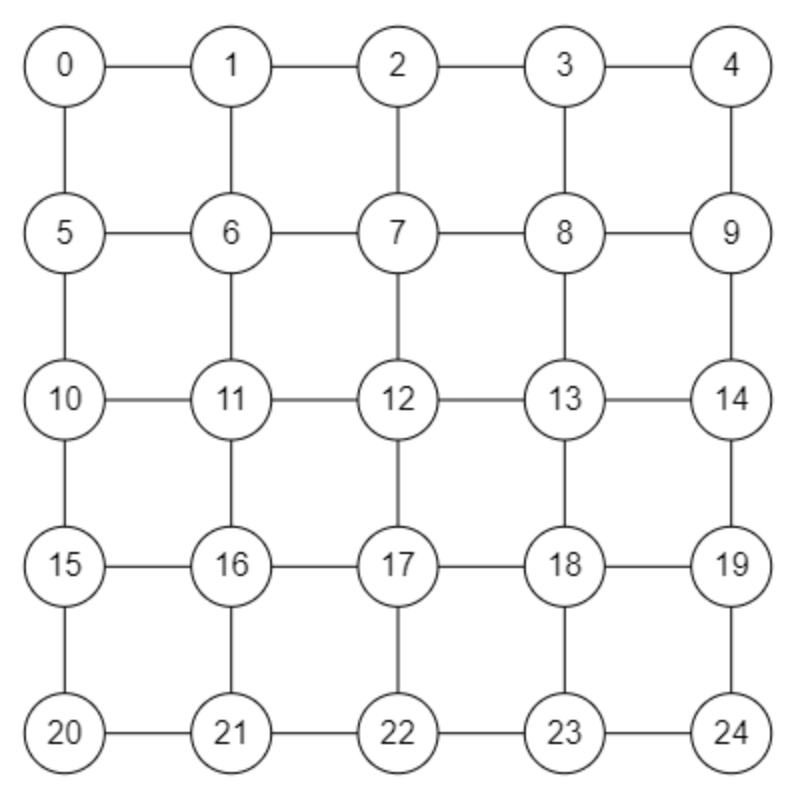
Wähle verschiedene Startknoten aus und führe die Breitensuche Schritt für Schritt analog durch. Kontrolliere dein Ergebnis hier.
Überlege dir einen Kurzvortrag, mit dem du jemandem die Breitensuche erklären kannst.
Taktikänderung
Eine alternative Traversierungsmethode ist die Tiefensuche, bei der man nicht zuerst in die Breite, sondern in die Tiefe geht.
- Recherchiere die Tiefensuche.
- Wende die Tiefensuche auf die drei oberen Graphen an.
Kleine Welt
Stanley Milgram führte im Jahr 1967 ein Experiment durch, aus dem das „Kleine-Welt-Phänomen“ hervorging. Recherchiere über dieses Experiment und bereite eine Präsentation vor.
Erklär dabei auch die Erdös-Zahl bzw. Bacon-Zahl.