
Warm Up
Führe die Breitensuche bei folgendem Graphen mit Start bei A durch.
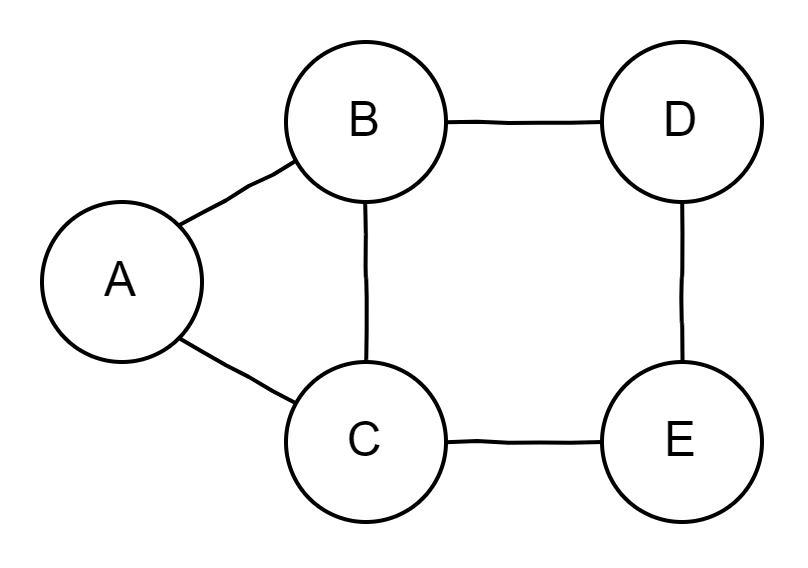
Du kannst hier (<- klick) deine Erinnerung auffrischen.
Entdecken
Kanten können ein Gewicht besitzen. Die Entfernung von A zu B ist jetzt nicht mehr 1 sondern 3.
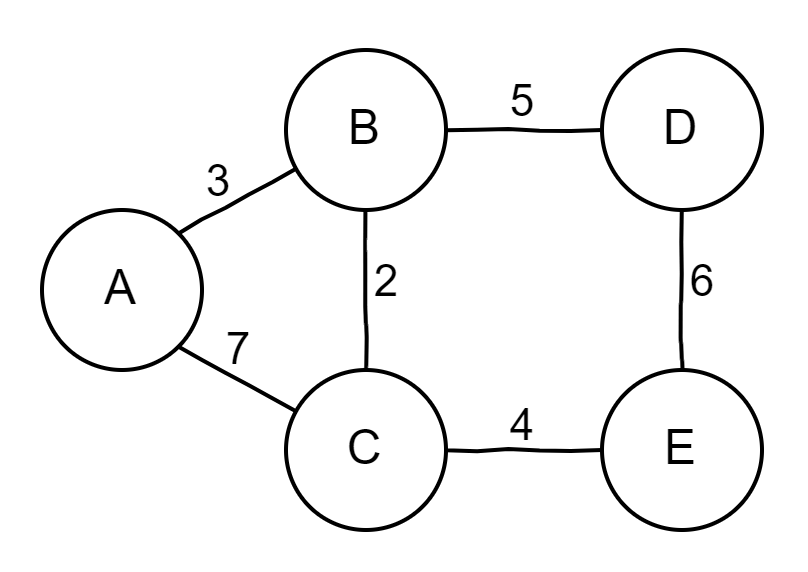
Führe wieder die Breitensuche durch und notiere hier die Entfernungen.
(Das sind nicht die kürzesten Wege!)
Dijkstra-Algorithmus
Edsger W. Dijkstra entwickelte den nach ihm benannten Dijkstra-Algorithmus, um die kürzesten Wege von einem bestimmten Knoten aus in einem Graphen zu bestimmen. Dafür benutzt er die Breitensuche mit ein paar zusätzlichen Ideen.
1. Entfernungen
Der Dijkstra-Algorithmus ermittelt stets die Distanz von einem Ausgangsknoten aus, indem die Kantengewichte entlang des Pfades addiert werden. Beispiel:

2. Wege können sich ändern
Wege über mehrere Knoten können durch geringere Gewichte kürzer sein. Daher variieren im Verlauf des Algorithmus die genutzten Kanten.
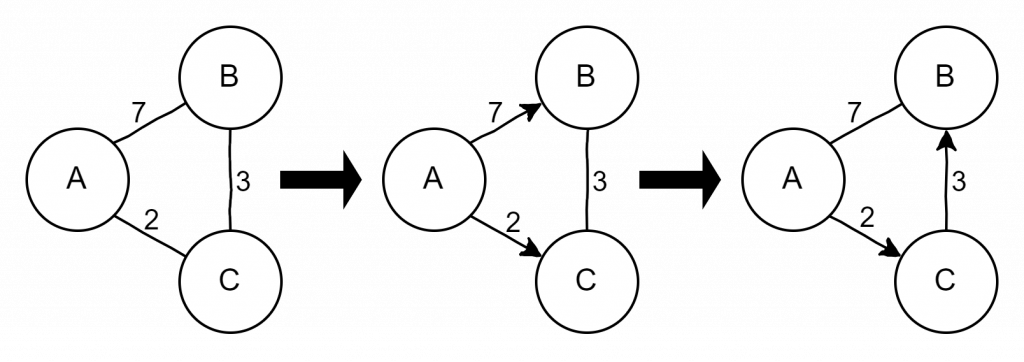
3. Priorisierte Warteschlange
In der Warteschlange wird nicht das erste Element entnommen, sondern dasjenige mit der geringsten Entfernung zum Startknoten.
Im folgenden Beispiel sind die momentanen Entfernungen an den Knoten notiert.
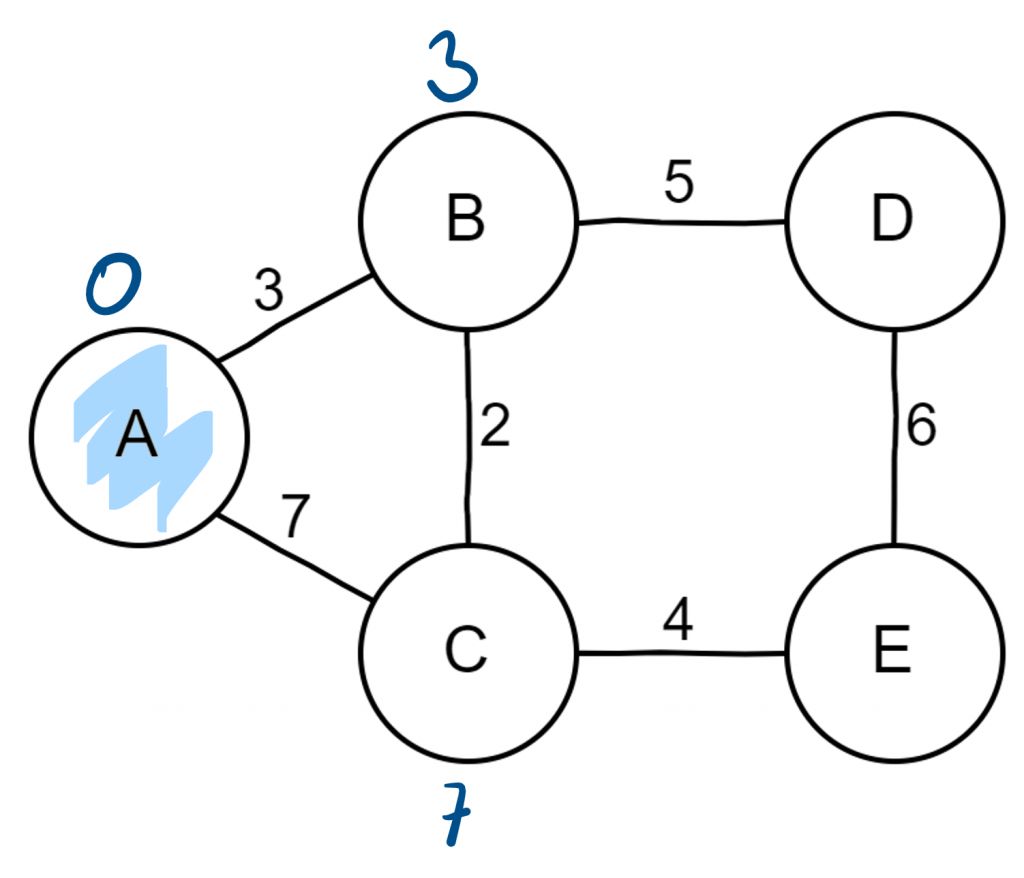
Alles zusammen
Hefteintrag
(Ja, abschreiben)
Der Dijkstra-Algorithmus
Mit dem Dijkstra-Algorithmus kann man in einem gewichteten Graphen die kürzesten Wege von einem Knoten aus bestimmen. Der Algorithmus baut auf der Breitensuche auf mit den zusätzlichen Elementen
- Entfernungen werden addiert,
- priorisierte Warteschlange und
- Kanten können sich ändern.
Übung
Führe den Dijkstra-Algorithmus mit Startknoten A aus.

Vertiefen
Edsger hat diese Woche im Unterricht gefehlt. Bereite einen kleinen Vortrag mit Beispiel vor, mit dem du ihm das Thema erklärst. Gehe auch auf den Unterschied zwischen Breitensuche und Dijkstra ein.