Die allgemeine Verschiebung von Funktionsgraphen

https://bthomsen.de/allgemeine-verschiebung/

Alle Aufgaben werden in Partnerarbeit bearbeitet. Eine Person ist der Pilot und bearbeitet die Aufgaben. Die zweite Person ist der Navigator und hat den Arbeitsauftrag offen und gibt Anweisungen, was zu machen ist. Nach jeder Unteraufgabe werden die Rollen getauscht.

Grundwissen

Öffne GeoGebra und gib die Funktion:

\[a\cdot sin(b\cdot (x-c))+d\]

ein. Achte auf die Malzeichen! Es sollte dann ungefähr so aussehen.

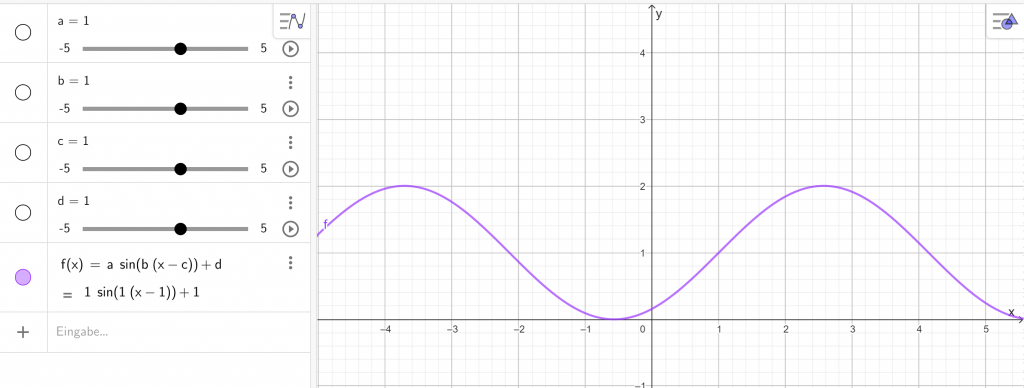
Zur Not kannst du auch die Vorlage hier öffnen.

Verändere die Parameter.

Entdecken

Öffne GeoGebra erneut. Gib die Funktion

\[f(x)=sin(x)\]

ein. Schreibe in die Eingabe danach

\[a\cdot f\]

ein. Es sollte jetzt so aussehen.

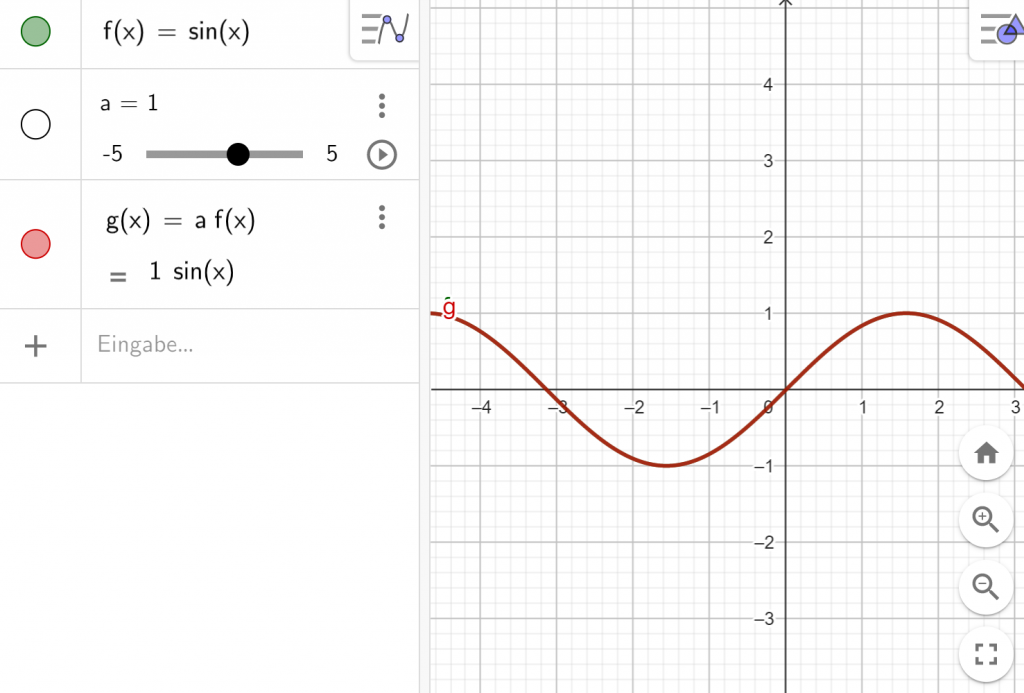
Verändere a! Was passiert?

Andere Richtungen

Ergänze die Zeichnung von der Aufgabe zuvor mit den Funktionen

\[f(b\cdot x)\] \[f(x+c)\] \[f(x)+d\]

Setze am Anfang die Parameter a und b auf 1 sowie die Parameter c und d auf 0. Verändere die Parameter nacheinander. Wie beeinflussen die Parameter die Funktion?

Auf andere Funktionen anwenden

Setze wieder die Parameter a und b auf 1 sowie die Parameter c und d auf 0. Verändere die Funktion f auf

\[f(x)=x^4 – x^2 \]

Verändere wieder nacheinander die Parameter.

Hefteintrag

(Ja, abschreiben)

Die allgemeine Verschiebung und Streckung von Funktionen

Man kann jede beliebige Funktion f(x) strecken oder verschieben.

Hinweis: 1/|b| ist die eine andere Schreibweise von

\[\frac{1}{|b|}\]

Übung

Nur ein Parameter muss bei den folgenden Rätseln geändert werden, damit der rote Graph auf dem grünen liegt. Finde ihn!

Rätsel Verschiebung 1

Rätsel Verschiebung 2

Rätsel Verschiebung 3

Rätsel Verschiebung 4

Rätsel Verschiebung 5

Die Kombination machts

Bei dem folgenden Rätsel müssen mehrere Parameter verändert werden. Welche?

Rätsel kombiniert

Hefteintrag Fortsetzung (ja, abschreiben…)

Der Graph der Funktion

\[k(x)=a\cdot f(b\cdot (x+c))+d\]

entsteht durch die Verschiebung und Streckung des Graphen von f entlang der Achsen.

Schatzsuche

Gegeben sind die Standardfunktion

\[lineare Funktion: f(x)=x\] \[quadratische Funktion: g(x)= x^2\] \[gebrochen-rationale Funktion: h(x)=\frac{1}{x} \] \[trigonometrische Funktion: i(x)=sin(x)\] \[Exponentialfunktion: j(x)=2^x \]

Jeder sucht sich eine Standardfunktion aus und verschiebt/streckt sie ganzzahlig. Sag deinem Nachbarn welchen Funktionstyp du genommen hast und den Graphen der Funktion und dein Partner muss dir die Parameter sagen. Wer zuerst die Parameter hat, gewinnt die Runde.