
Alle Aufgaben werden in Partnerarbeit bearbeitet. Eine Person ist der Pilot und bearbeitet die Aufgaben. Die zweite Person ist der Navigator und hat den Arbeitsauftrag offen und gibt Anweisungen, was zu machen ist. Nach jeder Unteraufgabe werden die Rollen getauscht.
Aufgabe 1
a) Öffne GeoGebra und gib die Funktion folgende Funktion ein:
Es sollten zwei Schieberegler für a und b erstellt worden sein. Es könnte so aussehen:

Sollten sich die Schieberegler nicht erstellt haben, füge sie eigenständig ein und gib danach den Funktionsterm ein.
b) Verändere die Schieberegler nacheinander von a und b. Notiere dir, welche Auswirkungen welcher Schieberegler hat. Benutze wenn möglich Fachbegriffe
Aufgabe 2
Verändere die Schieberegler, so dass die folgenden Graphen entstehen. Überprüfe eigenständig dein Ergebnis unter dem Graphen.
a)
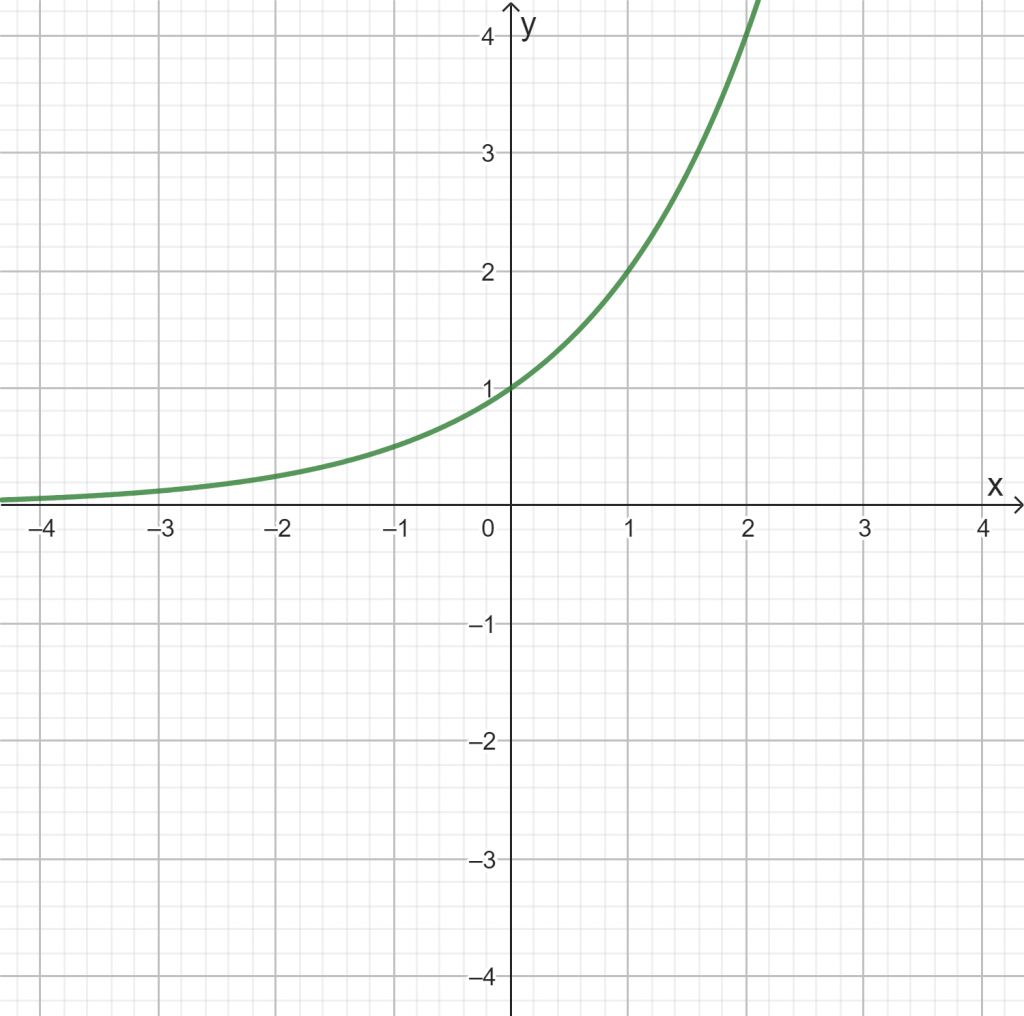
b)
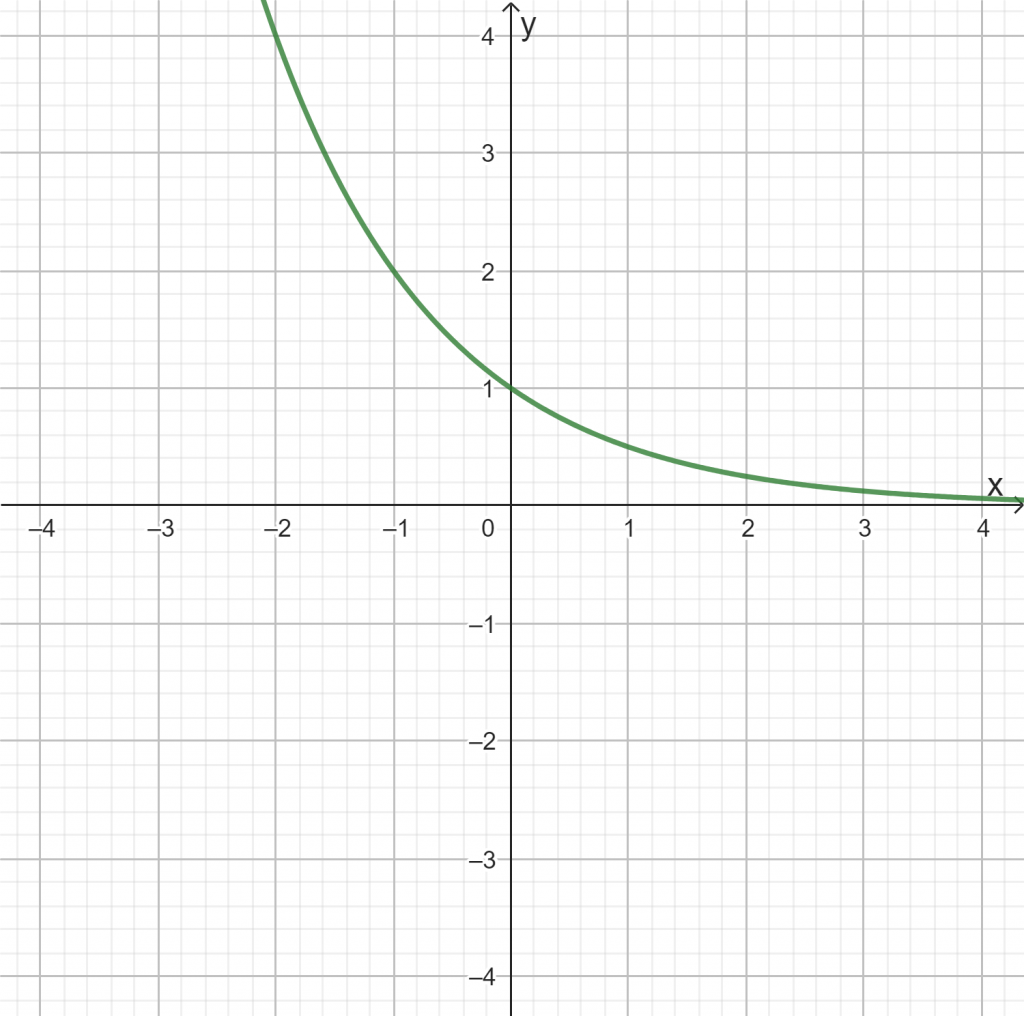
c)
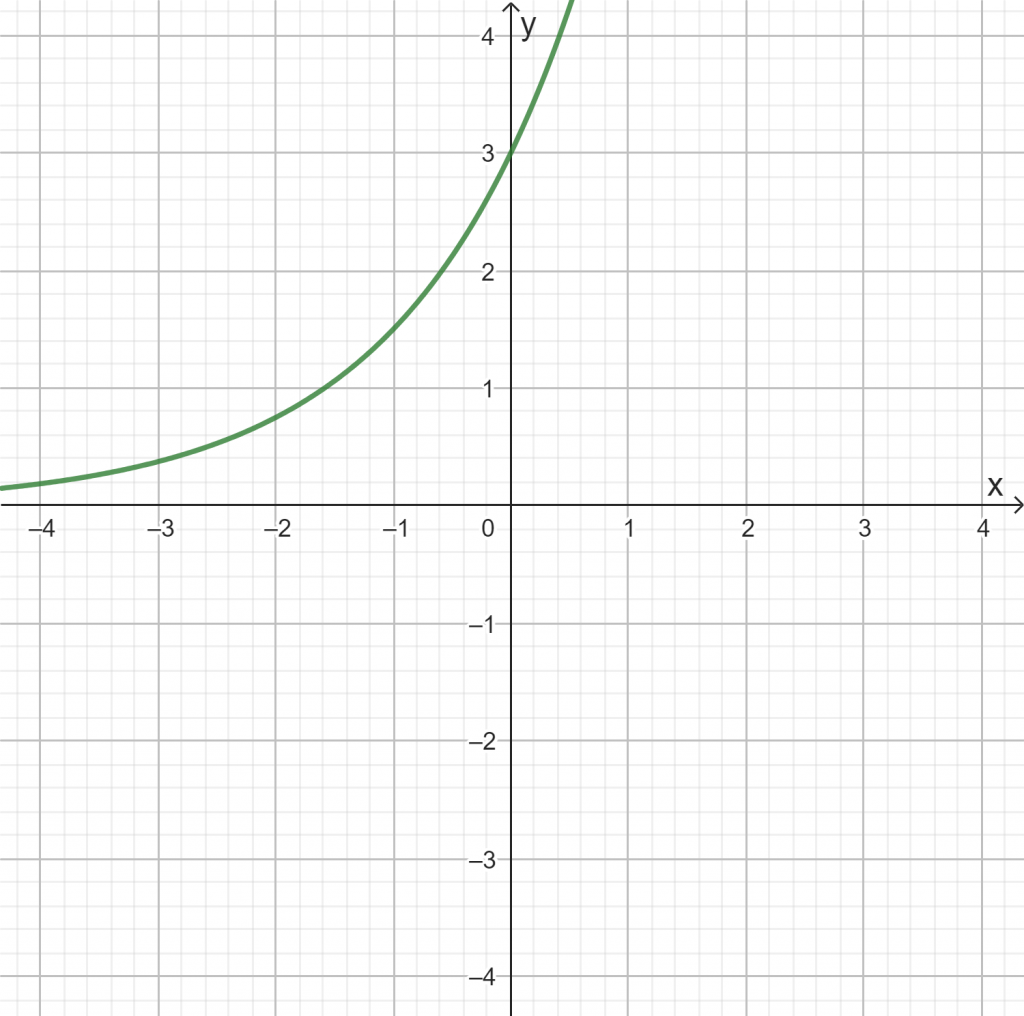
d)
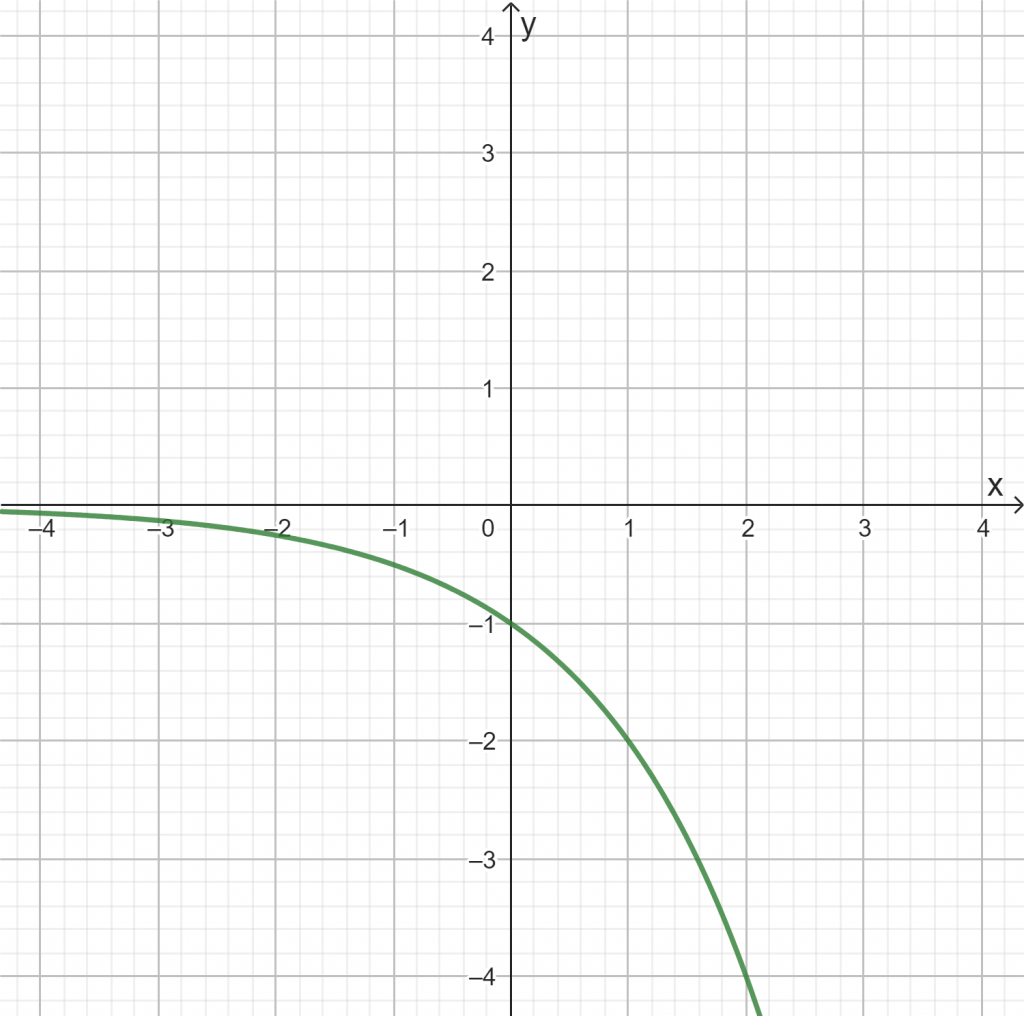
e)
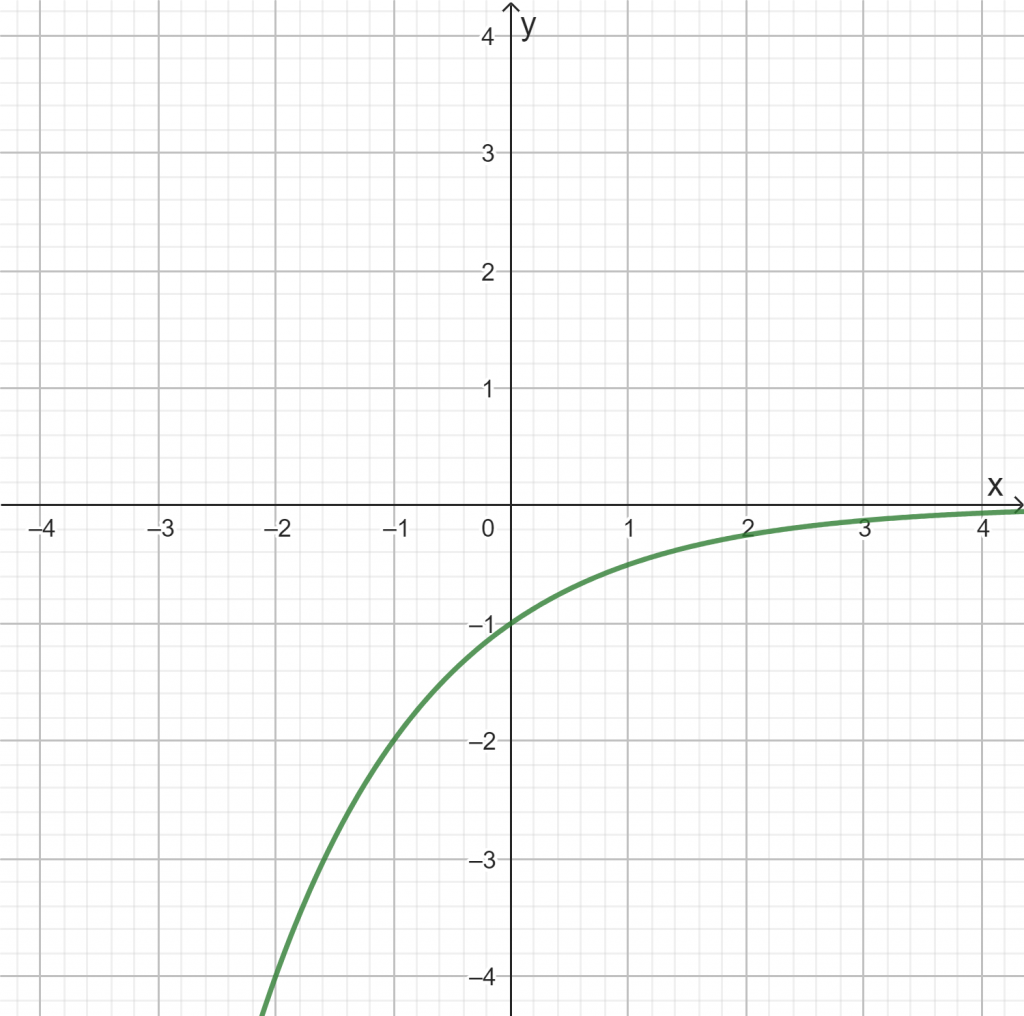
f)
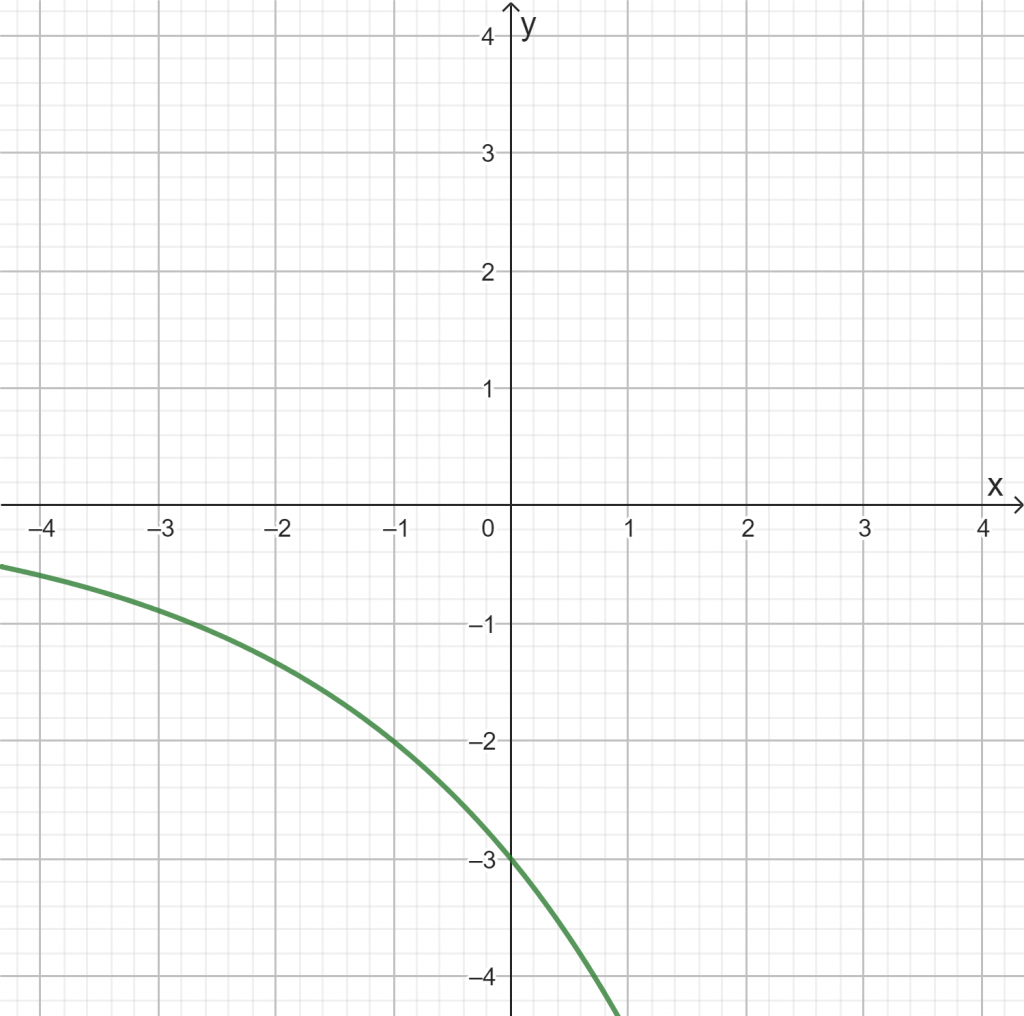
Aufgabe 3 (Hefteintrag)
(Ja… abschreiben!)
1.2 Die Exponentialfunktion
Eine Funktion der Form
heißt Exponentialfunktion.
Eigenschaften
Der Graph einer Exponentialfunktion kann in vier Möglichkeiten kategorisiert werden
(Ja… alles bis hierhin abschreiben)
Aufgabe 4
In der Definition der Exponentialfunktion steht
Stell die Schieberegler in GeoGebra nacheinander auf die ausgeschlossenen Werte von a und b. Erkläre deine Beobachtungen und warum man diese Werte ausgeschlossen hat. (Ja… schriftlich fixieren)
Aufgabe 5
Stell a auf eine natürliche Zahl und b auf 1. Wie verändert sich der Graph, wenn du b größer machst? Wie kann man das Verhalten bei negativen b beschreiben? Benutze Fachwörter!
Aufgabe 6
Zeichne die Graphen zu den folgenden Funktionen und vergleiche sie
Ersetze die 2 auch durch weitere Zahlen. Welcher Zusammenhang fällt dir auf?
Aufgabe 7
Notiere… ja… abschreiben
Bemerkung
Betrachtet man die Graphen von
und die Graphen von
Aufgabe 8
Zusatz
Wie viele schaffst du herauszufinden? Quiz in GeoGebra.
Hinweis: In GeoGebra werden Dezimalzahlen mit einem Punkt eingegeben. Die gesuchten Werte haben maximal eine Nachkommastelle.