
Plötzlich rollt ein Ball auf die Straße – ein Kind läuft hinterher. Du trittst sofort auf die Bremse. Doch wie lange dauert es, bis das Auto tatsächlich steht?

Der Reaktionsweg
Du siehst das Kind und bewegst den Fuß zum Bremspedal. In dieser Zeit fährt das Auto ungebremst weiter!
Wie weit, lässt sich mit der Faustformel:
Berechne den Weg bis du anfängst zu bremsen in Abhängigkeit von der Geschwindigkeit
Visualisiere den Reaktionsweg in GeoGebra. Gib dazu die obere Funktion im Grafikrechner (<- Klick) ein.
Der Bremsweg
Du trittst das Bremspedal – das Auto wird langsamer, aber es fährt noch ein Stück weiter, bevor es stehen bleibt. Wie weit das Auto während des Bremsens fährt, hängt von der Geschwindigkeit ab.
Die Faustformel zur Berechnung lautet:
Vergleich Reaktionsweg und Bremsweg
Der Reaktionsweg und der Bremsweg lassen sich nicht nur berechnen, sondern auch grafisch darstellen. So wird deutlich, wie sich die beiden Wege bei steigender Geschwindigkeit verhalten.
Zur Vereinfachung lassen wir die Division durch 10 in den Formeln weg.
Öffne Grafikrechner (<- Klick) und erstelle ein neues Koordinatensystem. Gib die Funktion für den Reaktionsweg ein:
Anschließend trägst du die Funktion für den Bremsweg ein:
Vergleiche die beiden Graphen miteinander. Beobachte, was passiert, wenn die Geschwindigkeit größer wird.
Die Normalparabel
Hefteintrag… Ja, abschreiben…
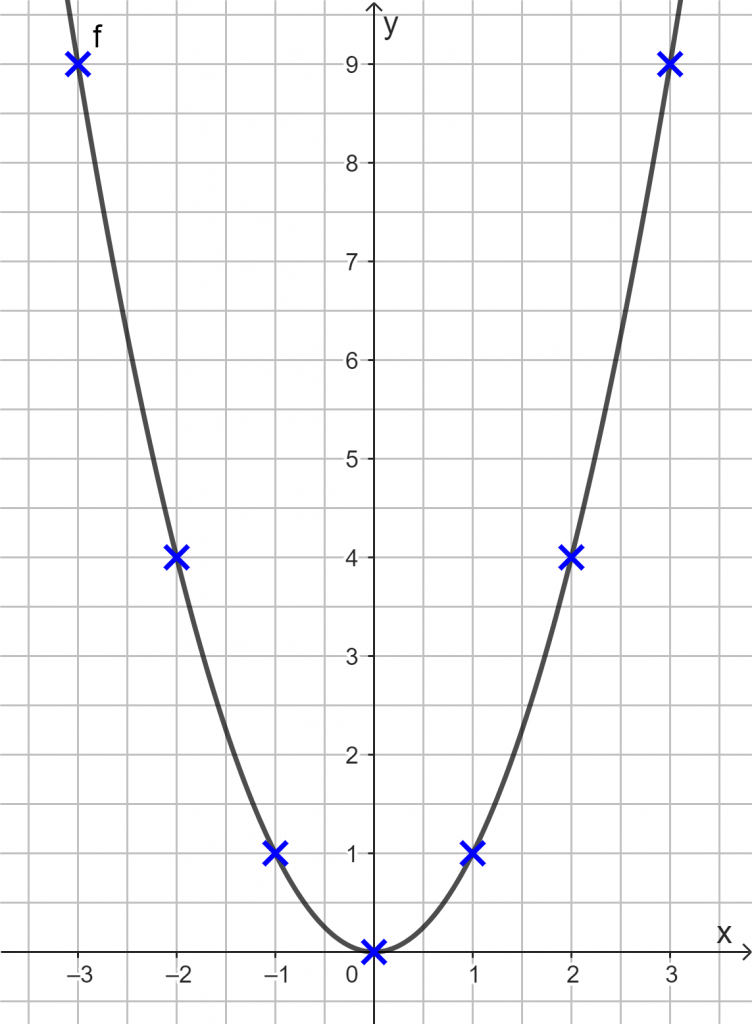
Der Graph G von f(x) = x² heißt Normalparabel. Diese wird immer wieder als Startpunkt für weitere Untersuchungen herangezogen. Der tiefste Punkt heißt Scheitelpunkt und liegt bei S(0|0). Die Normalparabel ist nach oben geöffnet und symmetrisch zur y-Achse.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| x² | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Basteln
Man kann fertige Parabelscheiben kaufen – doch wo bleibt da der Spaß? Viel spannender ist es, deine eigene Parabelscheibe zu basteln! Zeichne eine präzise Normalparabel, schneide sie aus und stabilisiere sie mit Pappe oder dickem Papier. So entsteht nicht nur ein nützliches Werkzeug, sondern auch ein echtes Unikat.
Herausforderung

Auf glatter Fahrbahn, wie bei Glatteis, verlängert sich der Bremsweg erheblich, während der Reaktionsweg unverändert bleibt.
Bei einer Geschwindigkeit von 20 km/h wurde auf einer vereisten Straße ein Anhalteweg von insgesamt 36 Metern gemessen. Bestimme den Faktor, mit dem der Bremsweg multipliziert werden muss, um auf dieses Ergebnis zu kommen.
Hintergrundwissen
Die oben beschriebenen weiten sind nur ungefähre Werte und sind natürlich von vielen verschieden Faktoren abhängig. Du kannst dich weiter informieren beim TÜV oder ADAC.