
Alle Aufgaben werden in Partnerarbeit bearbeitet. Eine Person ist der Pilot und bearbeitet die Aufgaben. Die zweite Person ist der Navigator und hat den Arbeitsauftrag offen und gibt Anweisungen, was zu machen ist. Nach jeder Unteraufgabe werden die Rollen getauscht.
Aufgabe 1: Gemeinsamkeiten
- Öffne GeoGebra Classic
- Erstelle einen Schieberegler n…
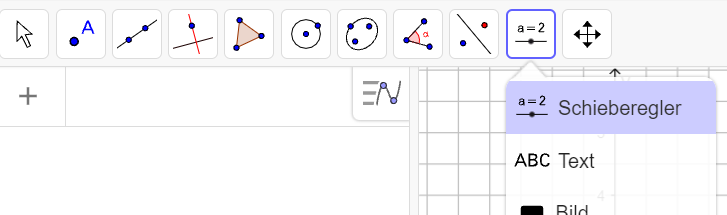
…mit:
- Ganze Zahl
- Min 1
- Max 30
- Schrittweite 1
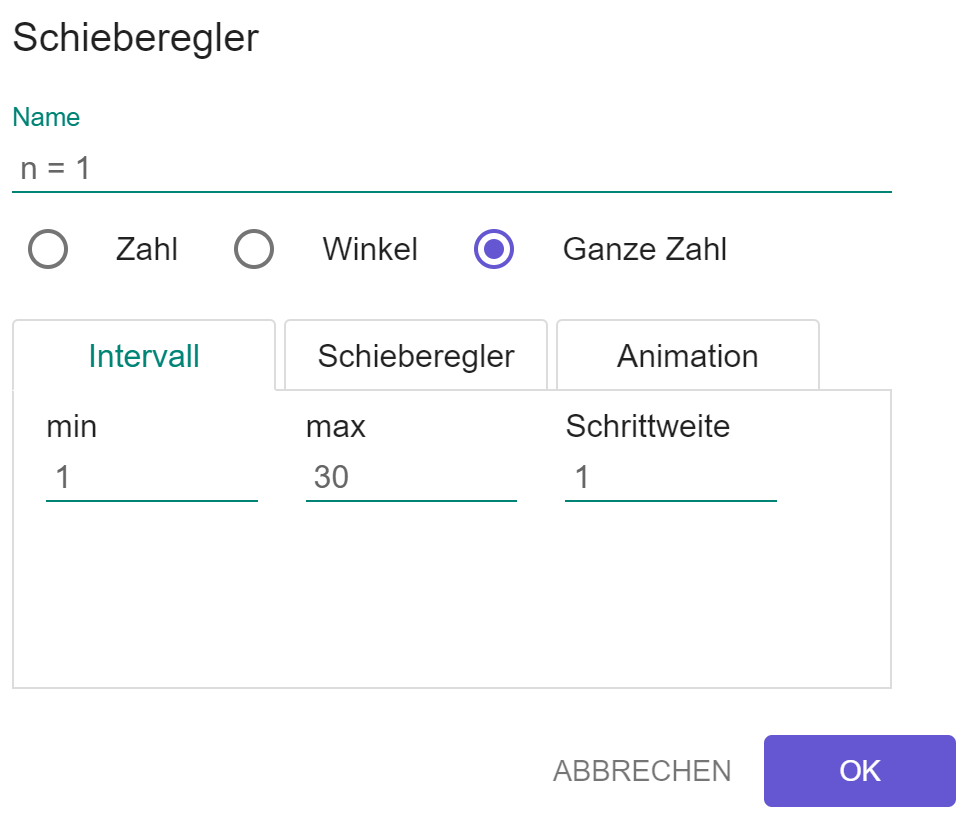
3. Gib folgende Funktion ein.
Es sollte dann ungefähr so aussehen
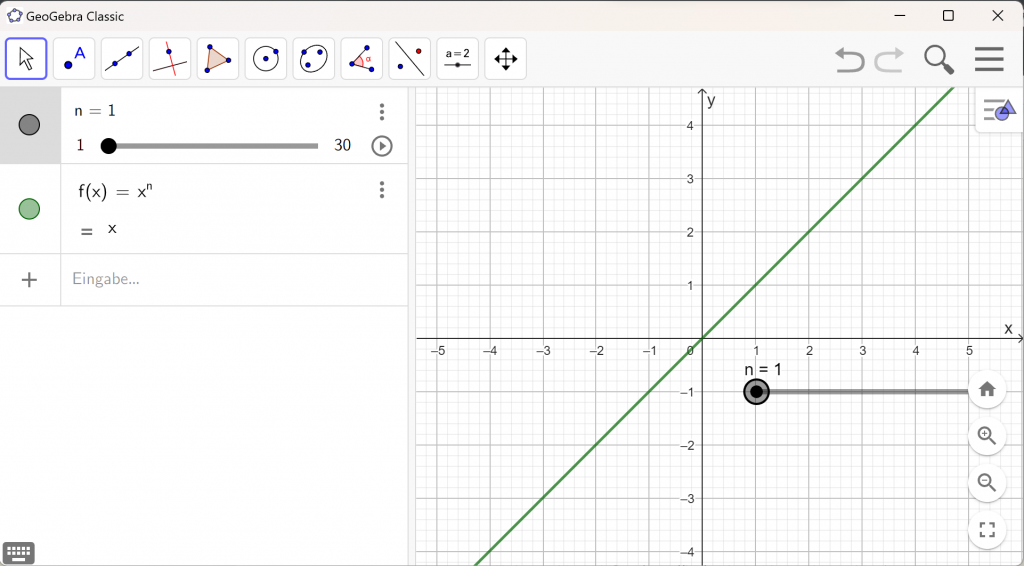
4. Verändere n. Solltest du starke Schwierigkeiten haben mit GeoGebra, so kannst du auch diese Vorlage benutzen: Vorlage
Untersuche die Graphen auf Gemeinsamkeiten:
- Beschreibe grob, wie jeder der 30 Graphen verlaufen. Erkennst du ein Muster?
- Alle Graphen haben ein paar Punkte gemeinsam. Welche?
Überprüfe anschließend deine Überlegungen
Aufgabe 2: Graphen sortieren
Sortiere die Graphen in die richtigen Kategorien ein.
Aufgabe 3: Symmetrie
Du hast bisher zwei Arten von Symmetrie kennen gelernt. Du kannst sie dir hier (<-Klick) noch einmal ansehen.
Welche Symmetrien besitzen Potenzfunktionen?
Aufgabe 4: Definitions- und Wertemenge
Die Definition einer Funktion:
Eine Funktion ordnet jedem x-Wert einen y-Wert zu.
Aber: Manchmal darf man bestimmte x-Werte nicht einsetzen – zum Beispiel, wenn man sonst durch null teilen müsste.
→Diese nicht erlaubten x-Werte gehören dann nicht zur Definitionsmenge (kurz D).
Und: Nicht jeder y-Wert kommt bei einer Funktion als Ergebnis heraus.
Zum Beispiel: Bei f(x)=x² kann nie ein negativer Wert herauskommen.
→ Solche Werte gehören nicht zur Wertemenge (kurz W).
Ordne den Graphen die richtige Wertemenge zu
Aufgabe 5: Monotonie
Die Monotonie eines Graphen gibt an, in welchem Bereich der Graph steigt oder fällt. Graphen können durchgehend steigen, aber auch nur abschnittsweise.
Finde mit deinem Graphen aus Aufgabe 1 heraus, wann welche Monotonie vorliegt.
Aufgabe 6: Hefteintrag
(Ja… abschreiben!)
Potenzfunktionen
Die Potenzfunktionen
Eine Funktion der Form
heißt Potenzfunktion n-ten Grades.
Eigenschaften
Skizziere die Graphen von Aufgabe 2 neben n ungerade und n gerade.
Aufgabe 7: Eigenschaften erkennen
Gegeben ist der Graph einer Potenzfunktion
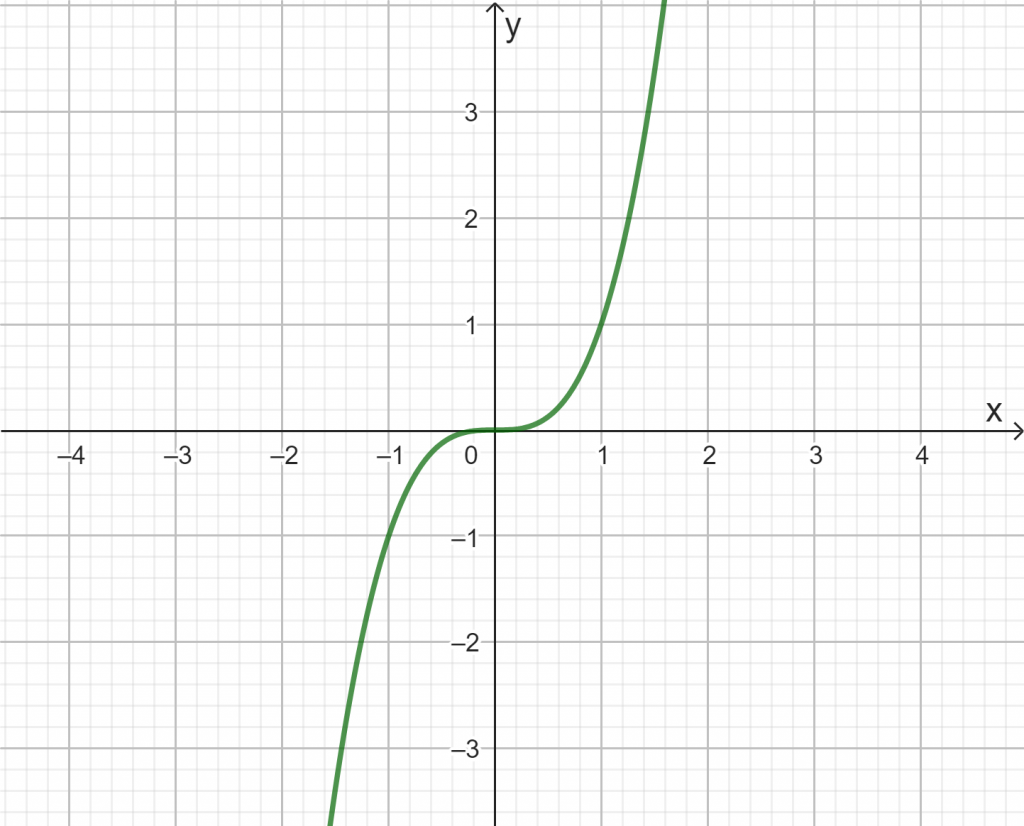
Aufgabe 8: Punkte bestimmen
Die folgenden Punkte gehören zu der Funktion
Aufgabe 9: für die Schnellen
a) Zeichne folgende Funktionen in ein gemeinsames Koordinatensystem
Beschreibe, wie die Funktion voneinander unterscheiden.
b) Analysiere Funktionen ungeraden Grades auf die gleiche Art.